I'm a big fan of fractals. In my free periods at sixth-form I'd spend time on www.easyfractalgenerator.com, designing elaborate complex polynomial functions then exploring the fractals that were generated from the recursive application of that function to areas of the complex plane. Unfortunately the website has been dead for a while now, but it was fun while it lasted.
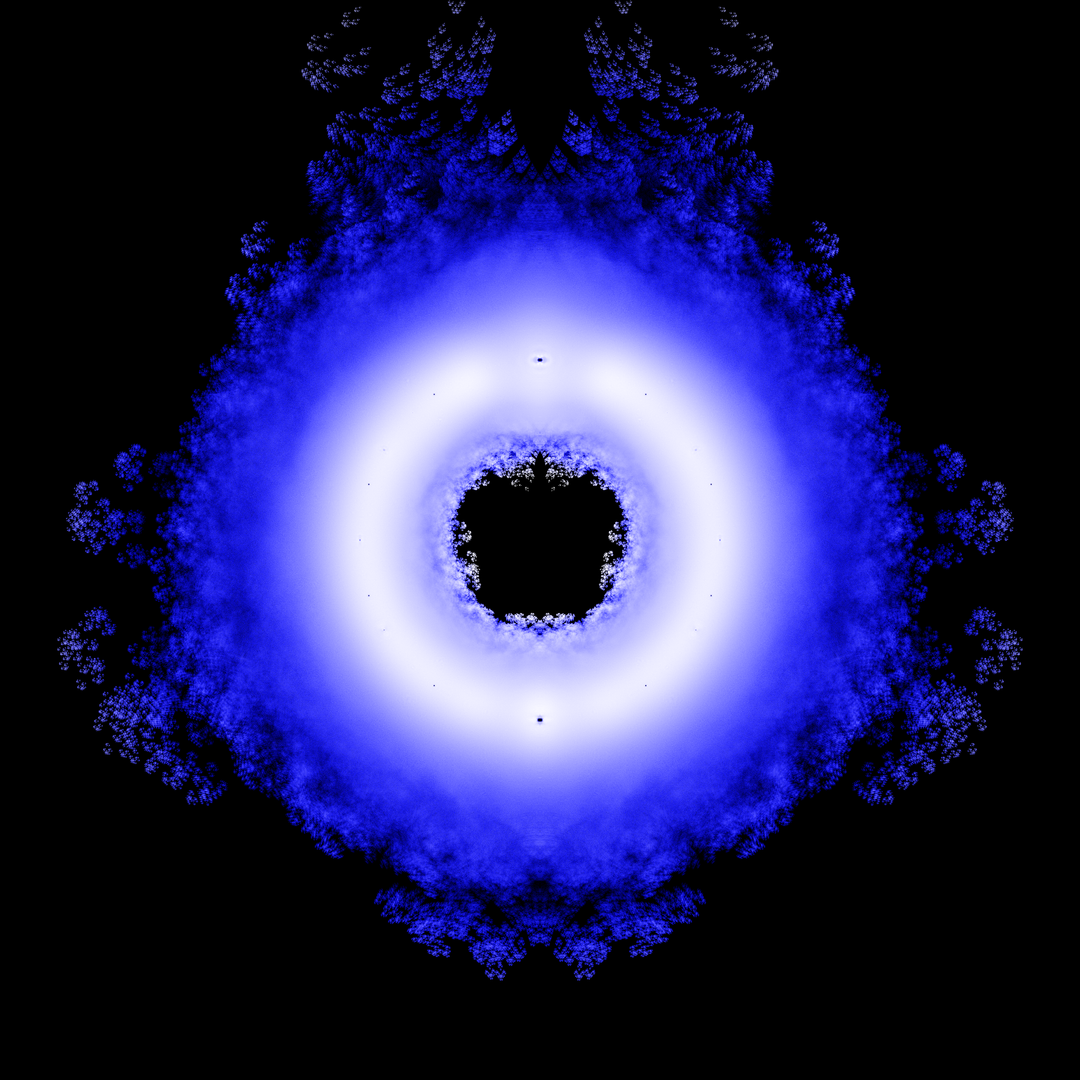
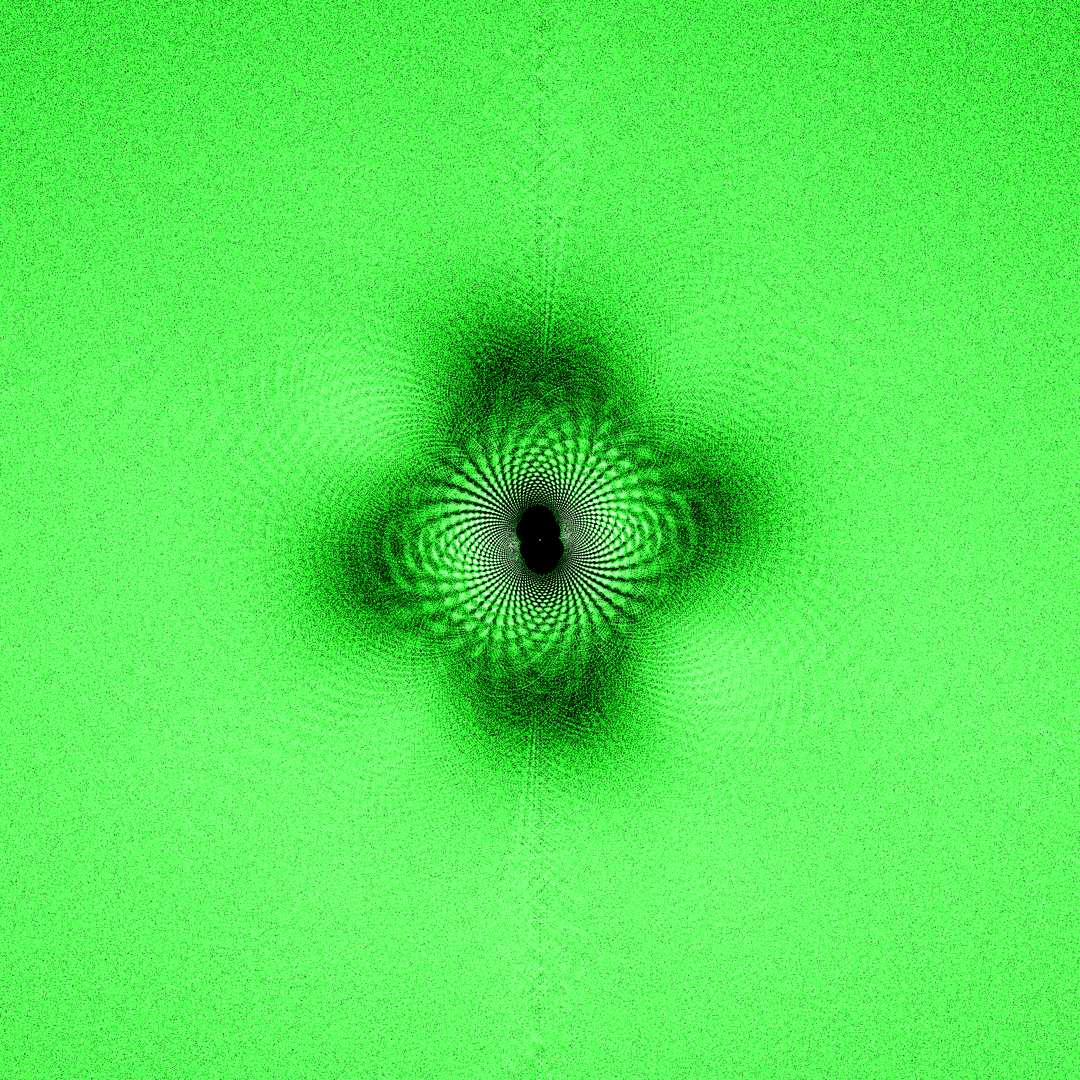
Around the same time I also found an interesting academic web page describing a novel fractal shape. This fractal was generated by finding the roots of polynomials with coefficients of +/- 1 (e.g. x^3 - x^2 + x - 1 = 0) and plotting them in the complex plane. Of course, you need a very large number of polynomials to plot this in high definition, up to the 24th order (x^24 +/- x^23 +/-...) to create the image below.

Reproduced from John Baez's site
There are some ornate fractal patterns in this image, dragon curves, self-similar feathery shapes, and voids around common roots like +/- 1. See the original website for more discussion of how and why these are generated.
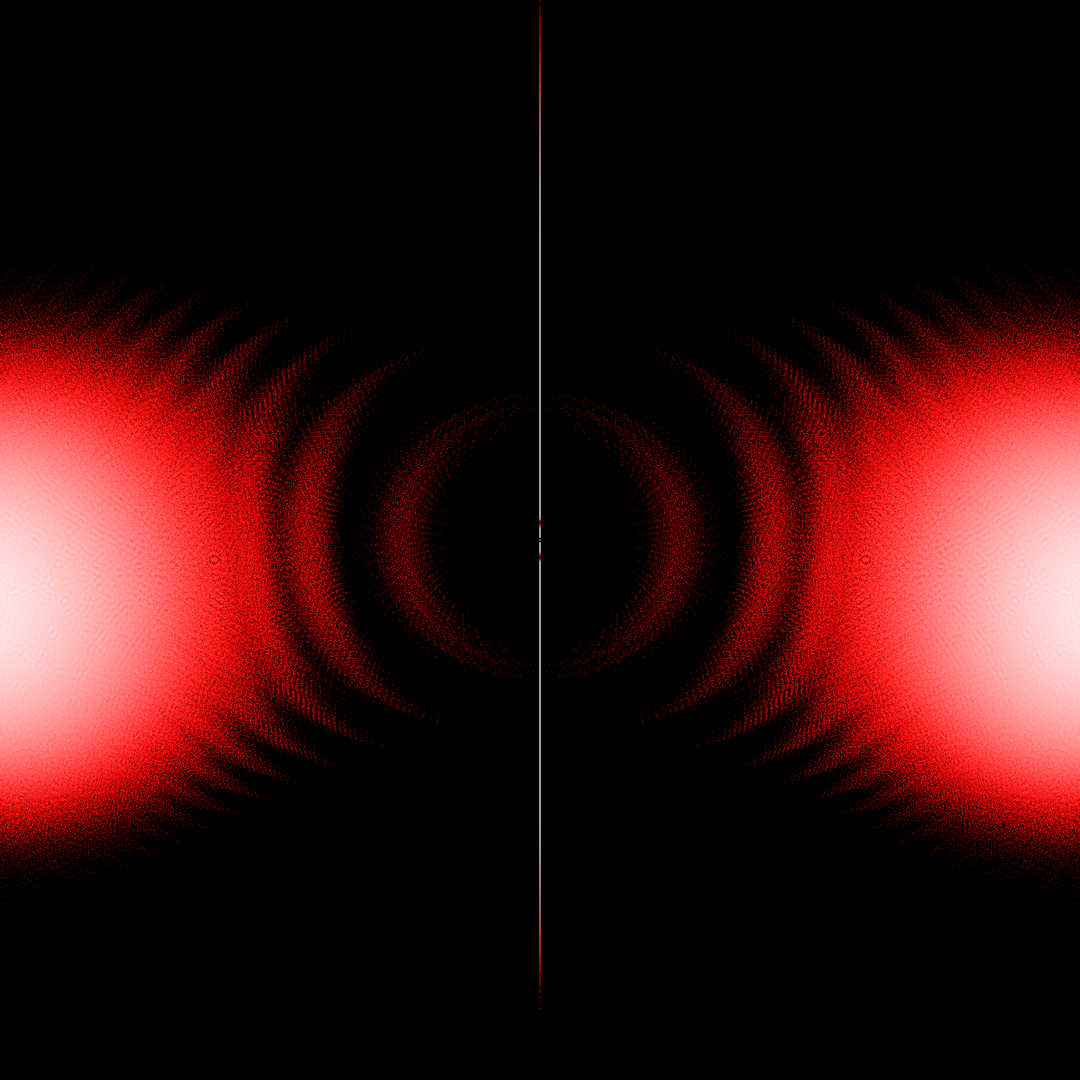
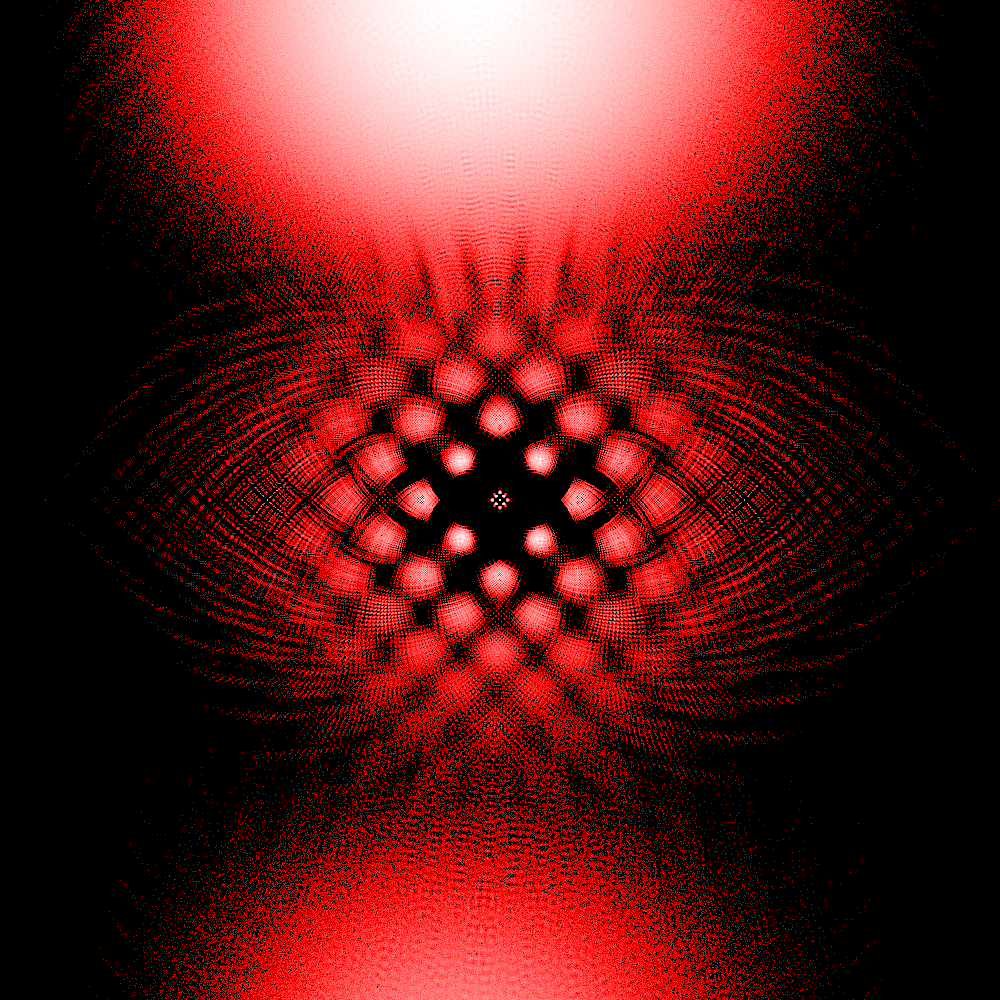
Most other online projects that I've seen reproduce this figure (sometimes to extremely high polynomial order), but I'm interested in how the shape changes as we vary the possible coefficients for the polynomials away from +/-1.
In some cases I kept just two possible coefficients but changed the scale/rotation between them in the complex plane. In others I extended to 3,4, or 5 possible coefficient values. The symmetry of the image reflects the symmetry in the coefficients. Using more coefficients drastically reduces the potential polynomial depth that you can achieve, because the number of polynomials increases exponentially as C^N for C different coefficients and polynomials of order N.
Each of the original images was at least 10000 x 10000 pixels and contains tens of millions of roots, with the largest that I made being 40,000 by 40,000 pixels across, I had to stitch that one together from tiles because my laptop didn't have sufficient RAM to create the image in one go.
I've rescaled the images below to a more reasonable size for a website, but if you want one of the originals then let me know and I can host it somewhere for download.
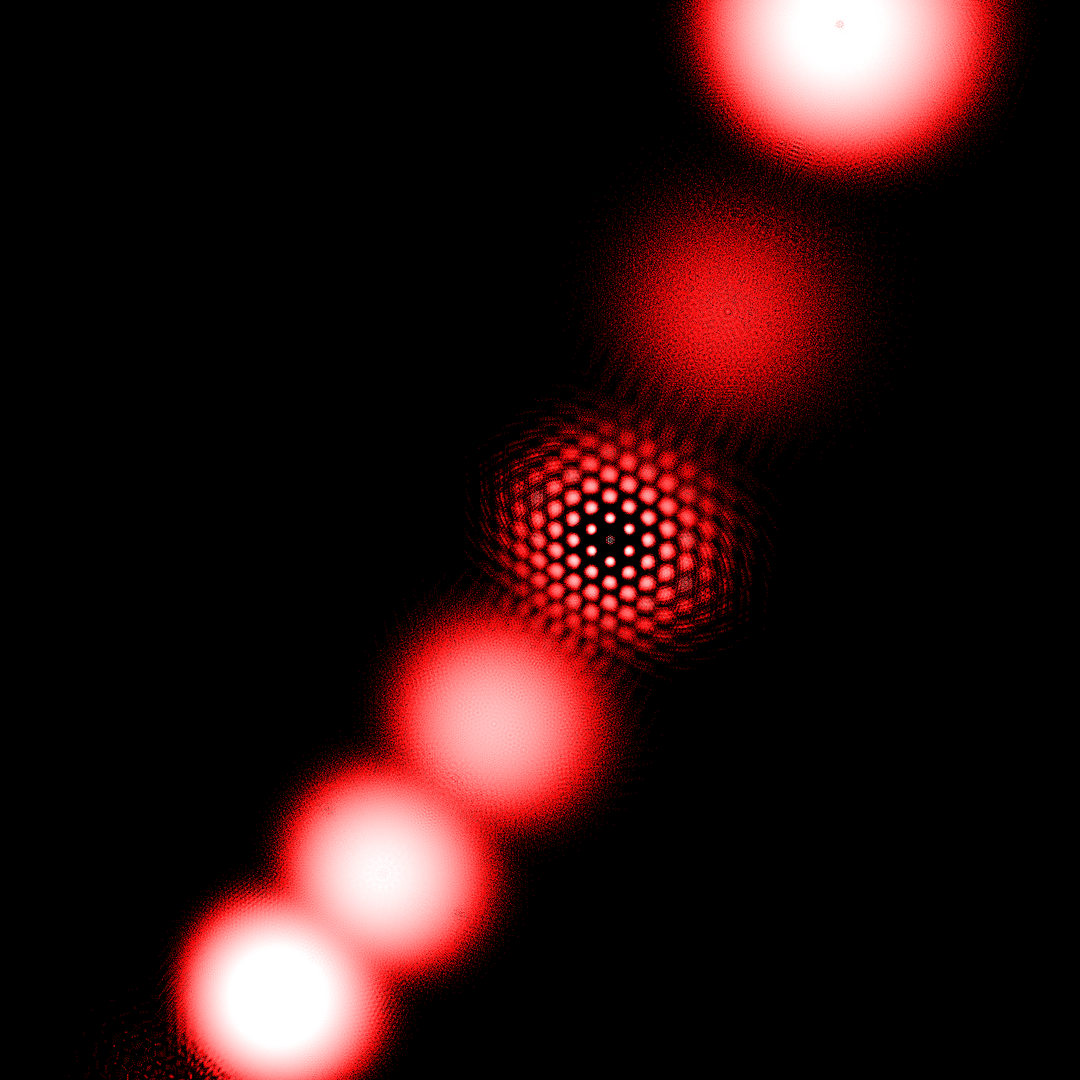
At the bottom of the gallery are some closeups from a couple of the images along with a video showing how the fractal evolves as you change the coefficient values in the polynomials, enjoy!