

In this post I'll go through my process for creating a program to simulate the evolution of river systems, including the impact of gravity, meanders and confluences, along with how I visualized them. This was more of an artistic simulation instead of a simulation of the underlying physics that leads to such emergent patterns.
I was inspired to undertake this project after seeing Harold Fisk's 1944 meander maps of the Mississippi river and Robert Hodgin's 'Meander' generative art project .
There were four main features of rivers that I wanted to include in my simulation:
1. Response to elevation changes
2. Meandering
3. Confluences at intersections
4. Branching & deltas
In all, I was able to achieve the first three of these criteria without needing to make a complex hydrodynamic simulation. Let's go through them in more detail.
To define my rivers I used a series of sampled points with x/y coordinates, rendered as a continuous line. Each line had a fixed "source" and "sink" which acted as tethers, fixing each end of the line, but allowing the centre to move freely.
I also defined a matrix containing elevation values at coordinates in the area I wanted to use. This matrix was fixed as I didn't simulate the impact of erosion on the terrain in the map. Natural shaping of the ground around the rivers could perhaps be a future extension to the project.
The gradients of the elevation matrix in the x- and y-directions were saved and used to apply forces to the sampled river channel points. At each timestep, a point would be moved by a force proportional to the local elevation gradient. The line would then be resampled to ensure even spacing between the points. This keeps a manageable curvature in the line by regularly sampling and is especially useful when we move on to meanders and confluences.
This method of moving the river under gravity is simple and easy to implement, but it isn't necessarily the best for a realistic simulation. Rather than gravity causing a river to straighten out down a steep slope, it would instead cause the existing river channel shape to be translated downhill over time. In the future, I might change the gravity scheme to one that aligns the river channel with the local gradient, rather than on that simply moves the channel in the direction of the gradient.
Also, this setup means that each river must be created with an extant channel between the source and sink. If the initial river channel crosses a saddle-point in the elevation map, then the river cannot escape to find the true lowest-energy path between source and sink and will inevitably travel uphill for a portion of its journey.
Gravity is by far the simplest feature to implement, after this it gets a little more tricky. Meandering was the next task on my list.
The physics behind the formation of meanders is complex, involving helicoidal secondary flow patterns that increase erosion on the outside of bends and deposition on the inside. I did not want to simulate this full process (my river channels are one-dimensional!) and so I limited myself to explaining this phenomenon by simply using the local curvature of the river channel with no underlying physics.
The meander force was created with a combination of the tangent to the river channel plus the outer bitangent, proportional to the local curvature of the channel at that point. This is essentially the same method as Hodgin's Meander project. I scaled the relative strengths of the forces until the result looked reasonable.
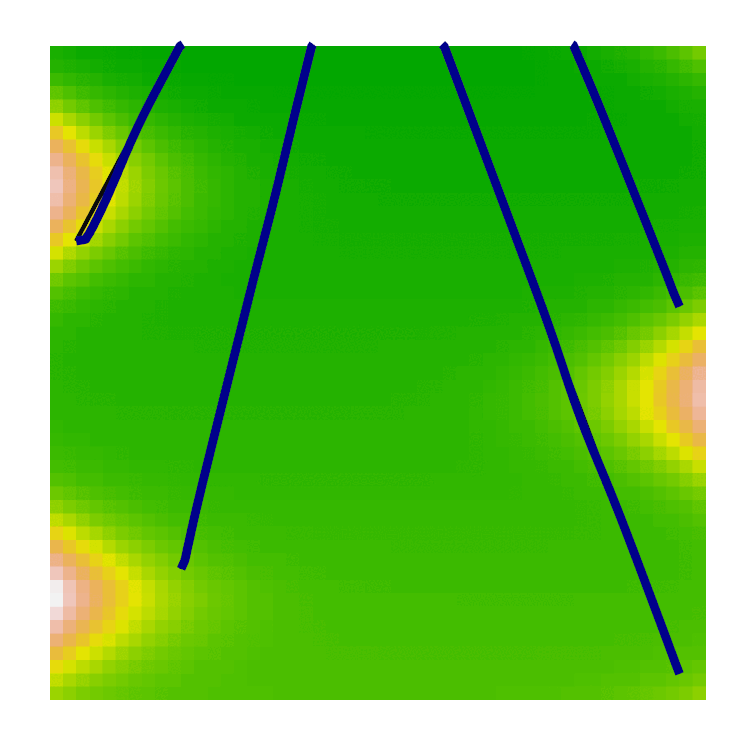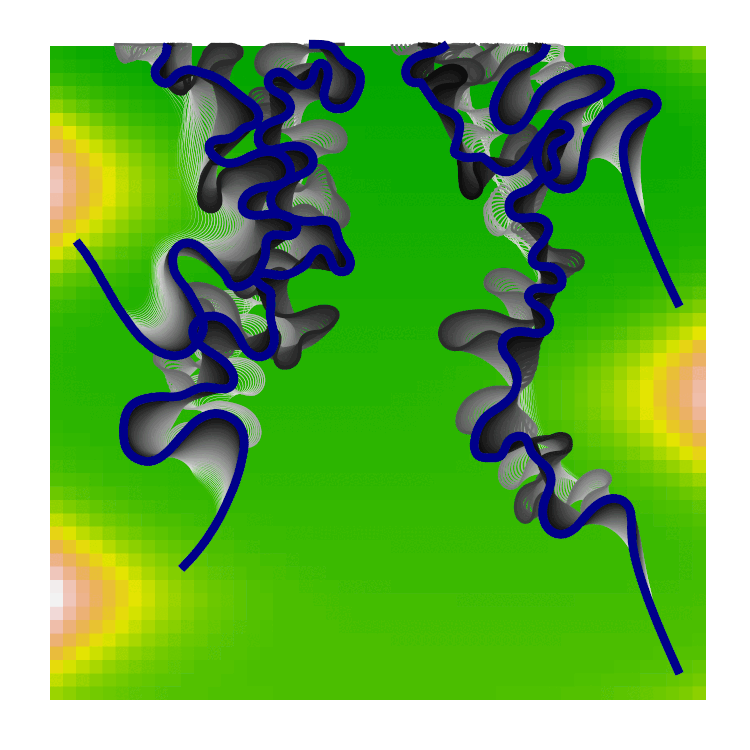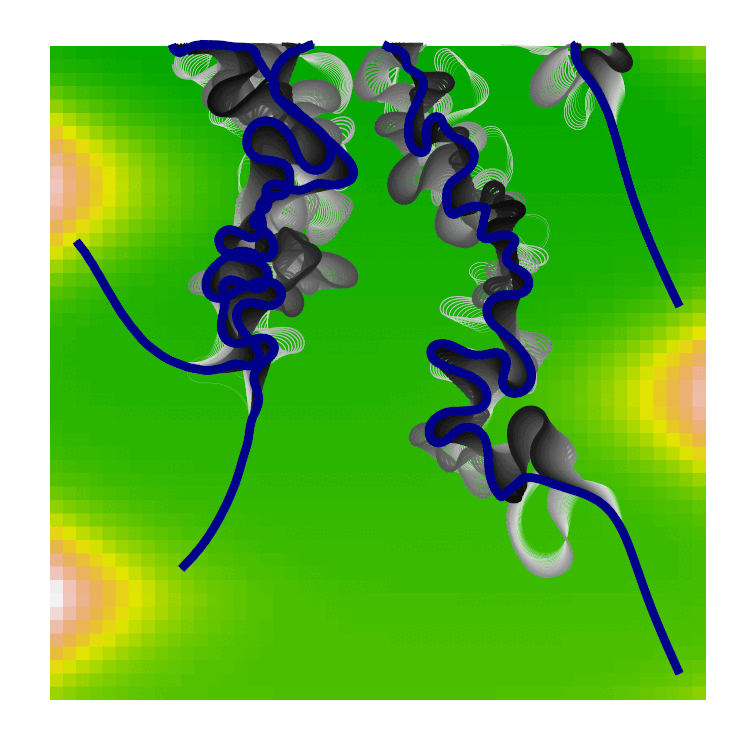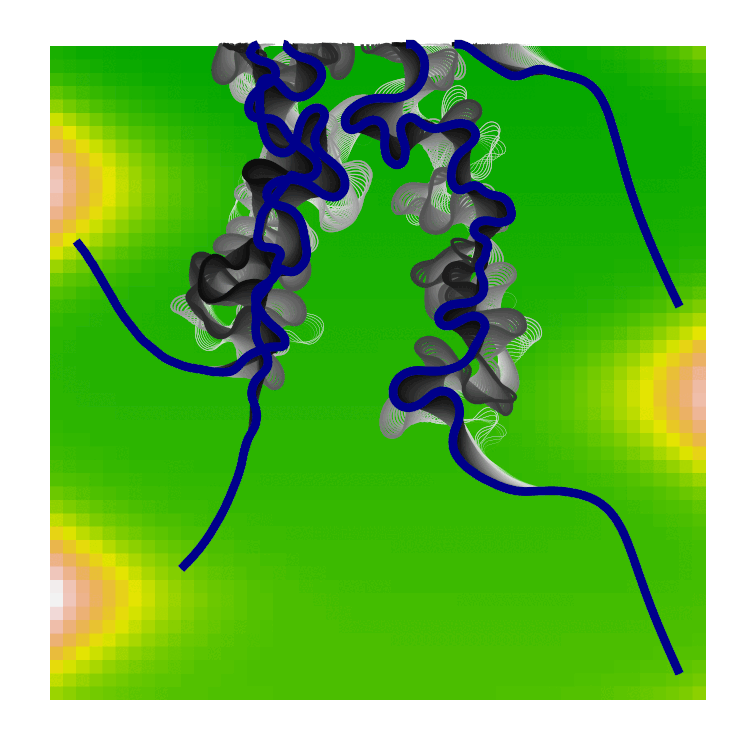
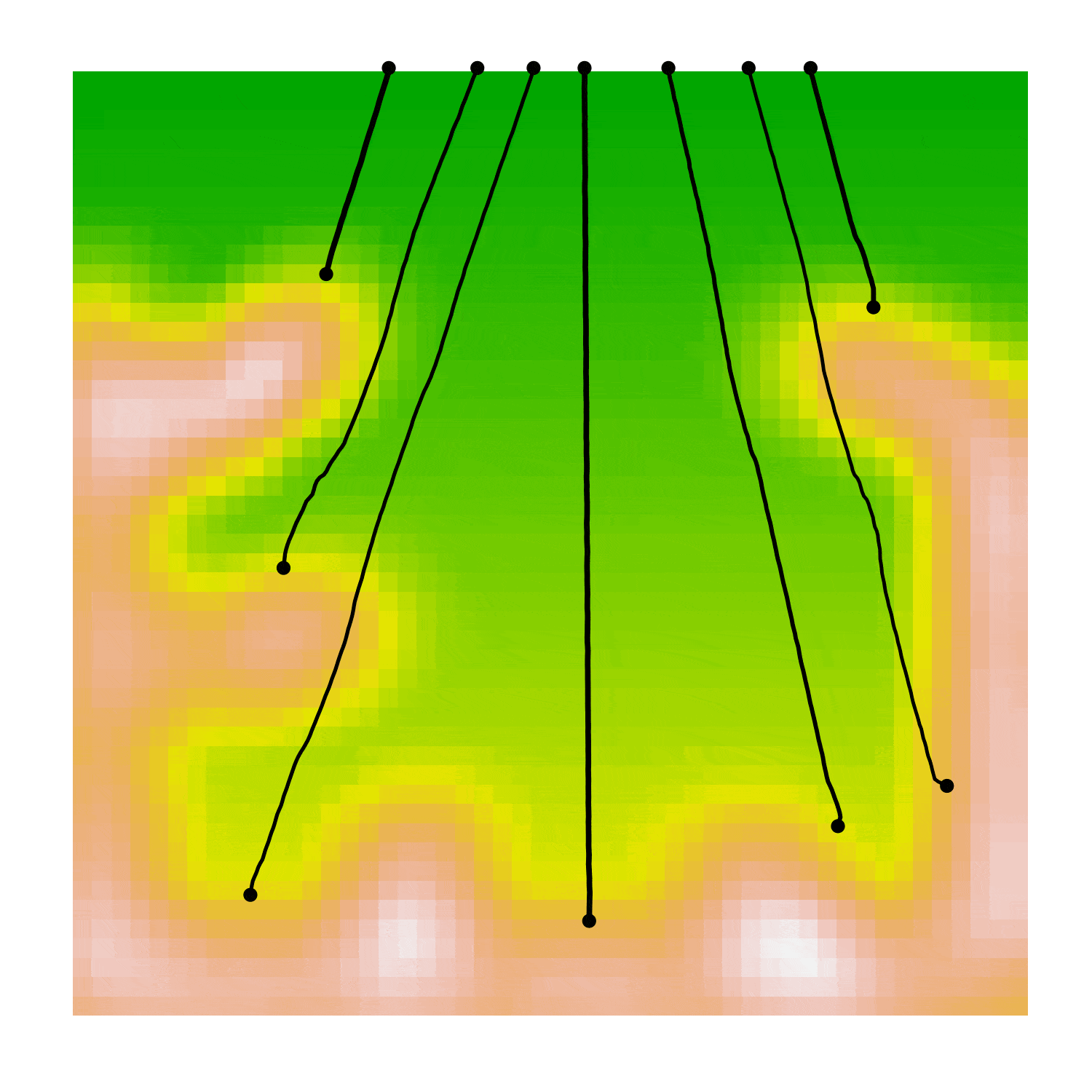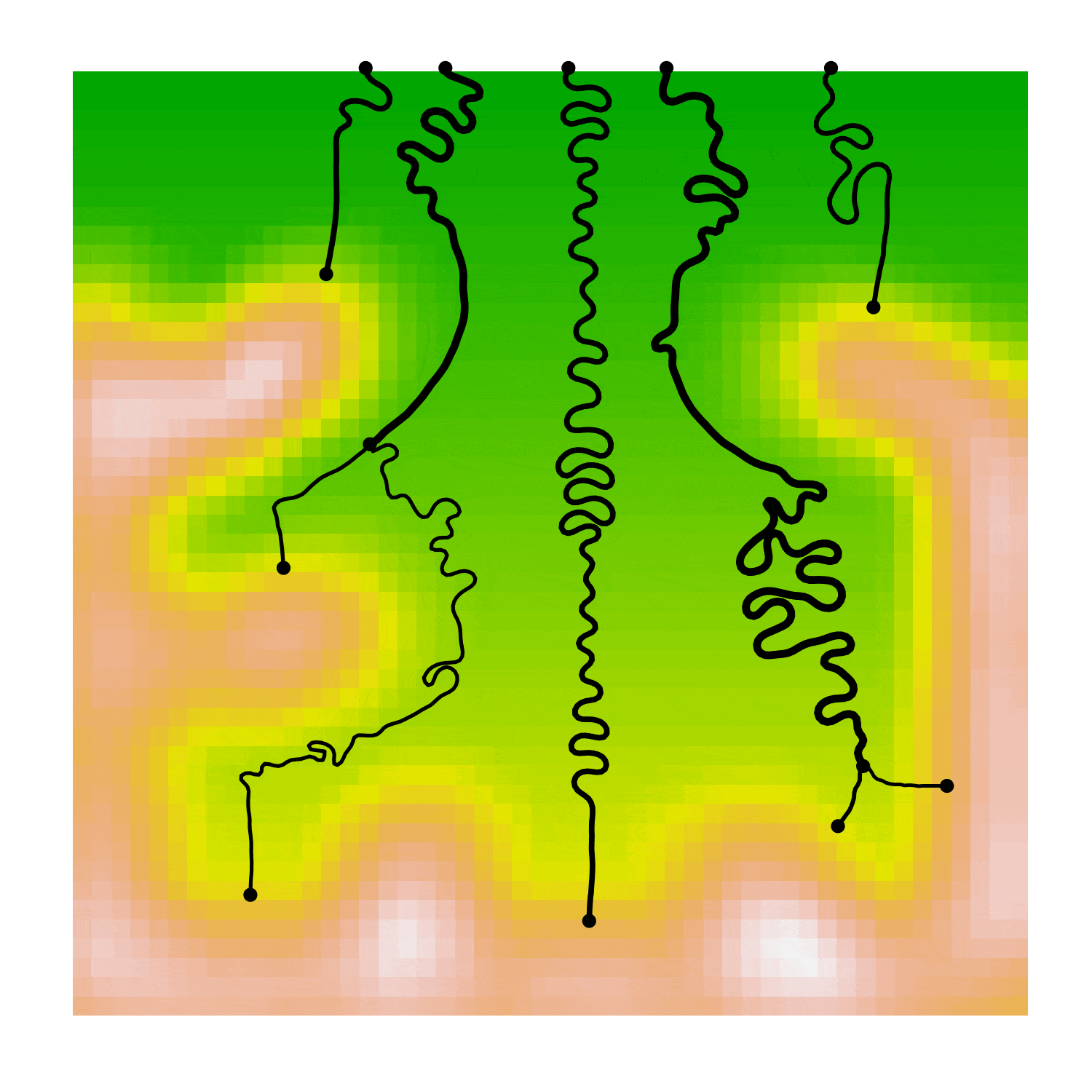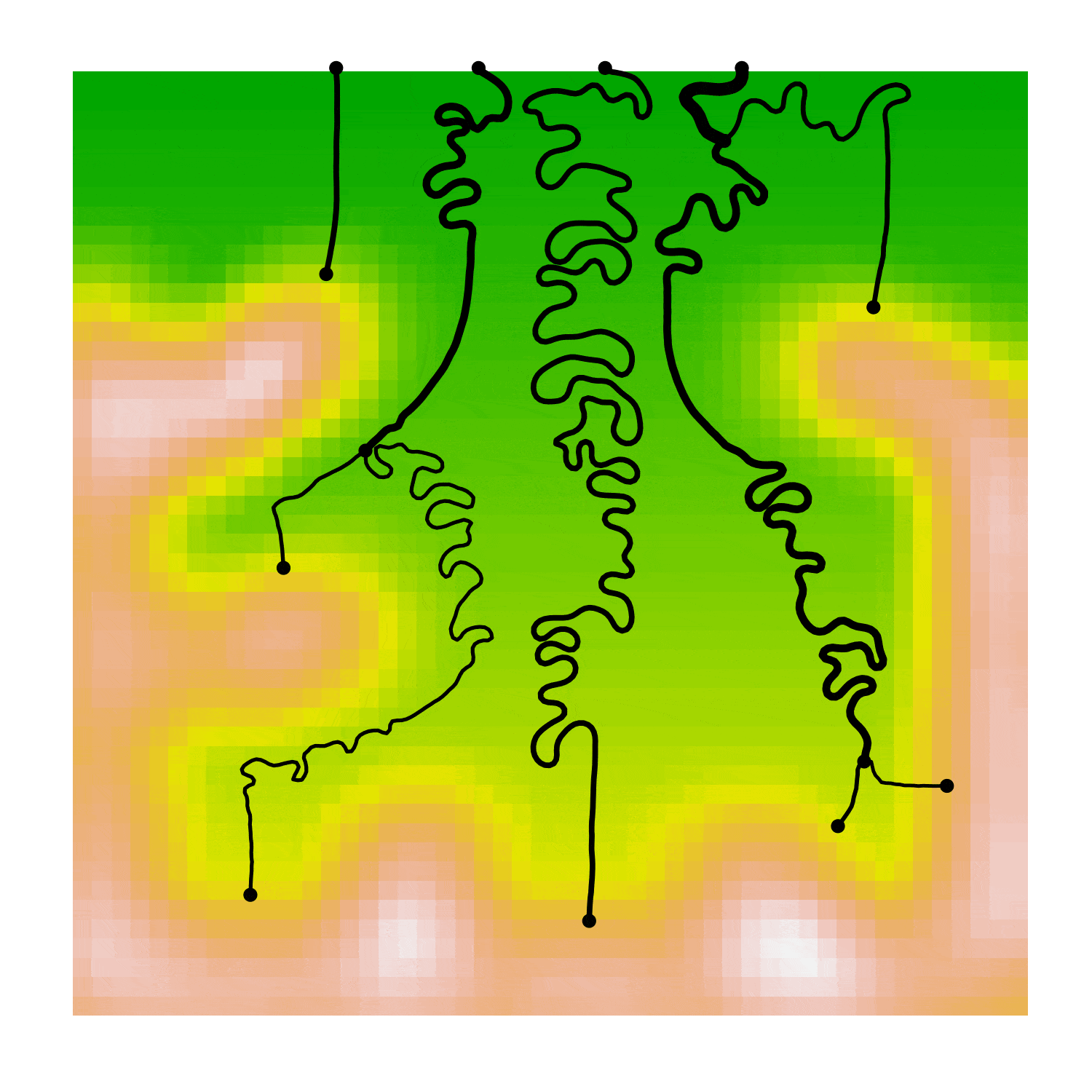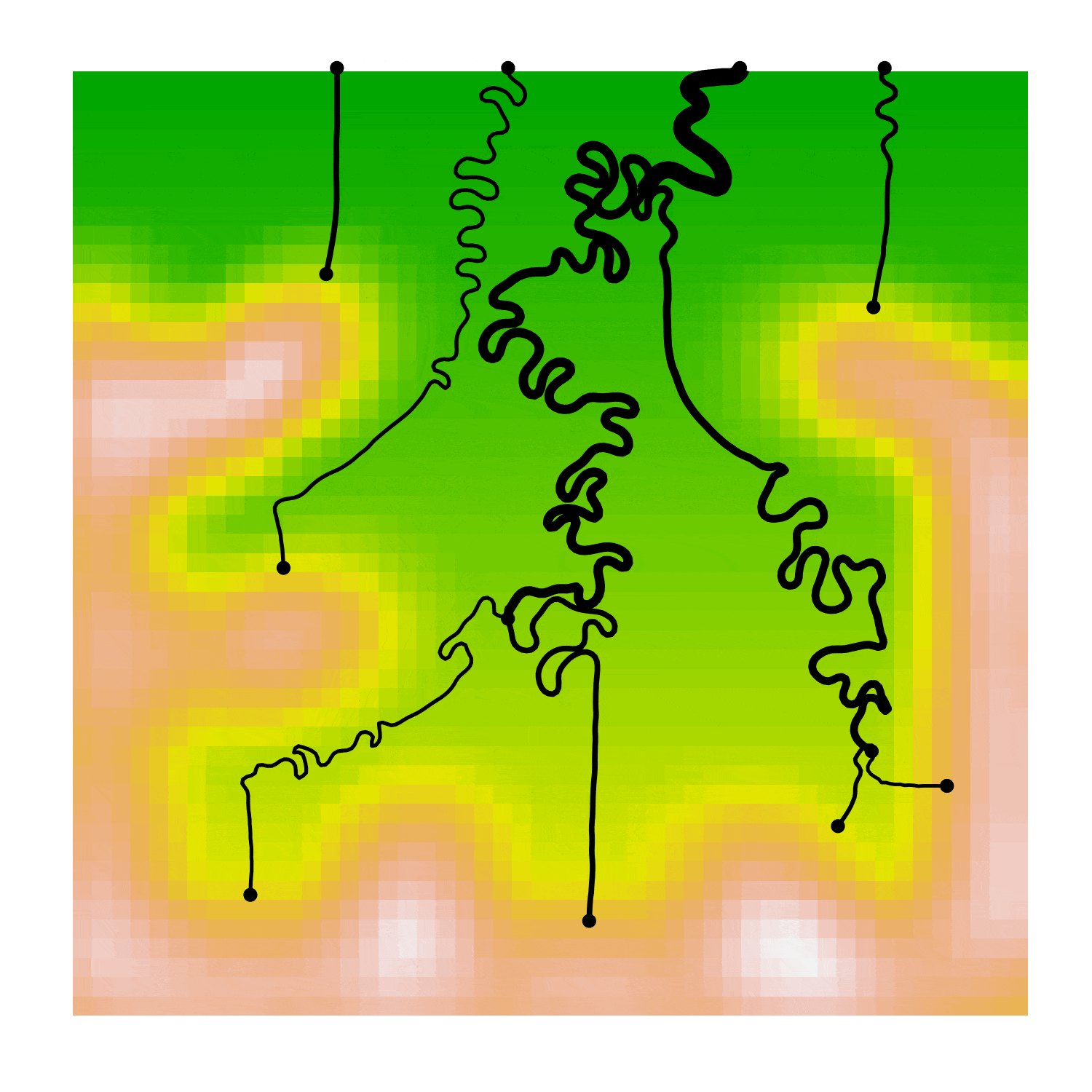
The image below shows a river channel after including meanders but no collision detection. The underlying colour shows the elevation map that I used. The river initially flows in a straight line steeply downhill then meanders form in the flat valley bottom as the river winds around itself.
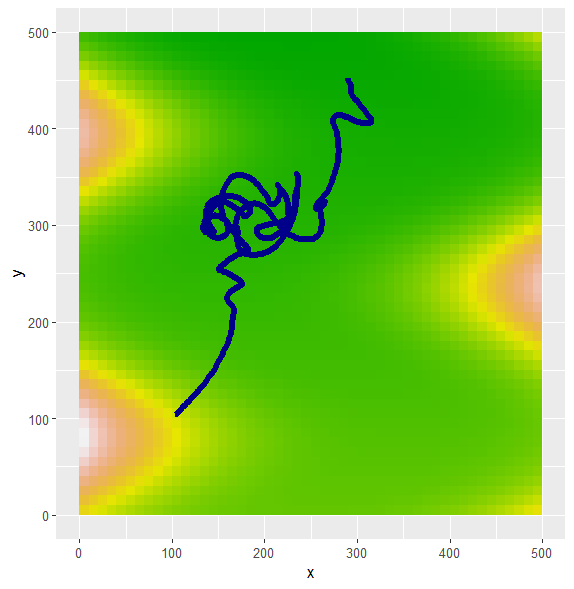
Next, self-collisions of the river channel could be added, upon a collision, the interstitial segment is removed. This is the characteristic cutting that leaves ox-bow lakes behind in meander belts. The gif below shows the evolution of river channels with self-collisions and each channel leaving a shadow of its past evolution. Note that there are currently no collisions between channels, which causes them to overlap.
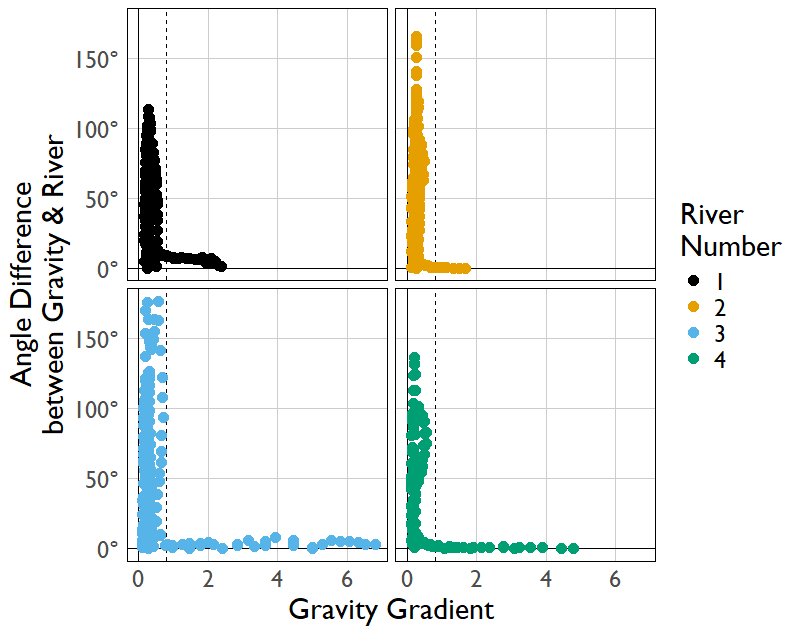
Meanders only form when the gravity gradient is sufficiently low, otherwise the river channel is moved downhill faster than meanders can form. We can see in the graph below that the flow aligns with gravity unless the gravity gradient falls below a threshold at which point meanders can cause large differences between the elevation slope and the river channel.
The addition of mergers between river channels was a big step up in the complexity of the code. It meant that I couldn't just use independently defined river channels and naively update them one after another. I needed to build a larger structure to handle the river network that could be manipulated when mergers occurred.
I represented my river network as a graph, specifically a directed acyclic graph (DAG). The graph is directed because the rivers flow from source to sink, and the graph is acyclic because rivers do not have loops in them where the downstream flow rejoins itself upstream. This is because if such a cycle existed, the river would quickly realign to skip the cycled portion and simply flow directly downstream instead. This acyclic nature is why meander cutting results in a detached oxbow lake, rather than continuing the river through the old meander channel when a better option is now available to the flow within.
Each portion of the river channel is represented as an edge of the graph. Nodes of the graph can be sources, sinks, or junctions between channels. The volume of water flowing through a particular river channel can be represented as a property of the edge. The graph can automatically calculate the volume through each channel based on the upstream volume from each source. The physical location of the river channel in space is also attached as a property of each edge of the graph.
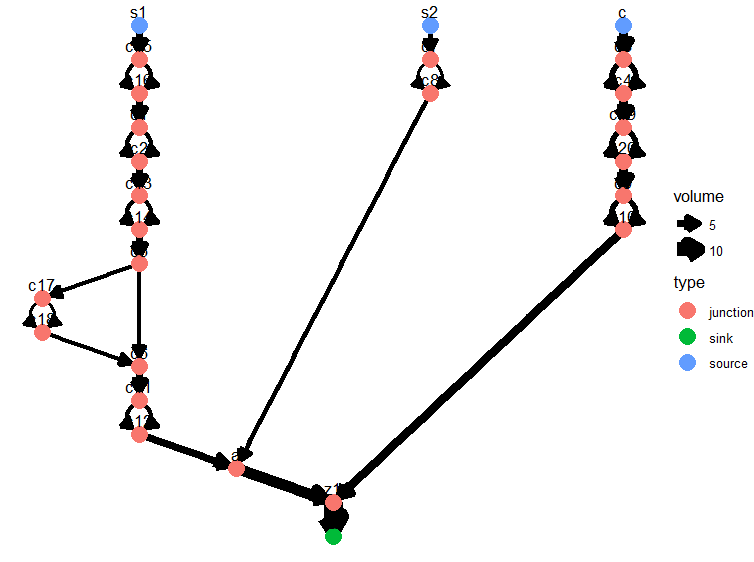
The graph below is a schematic of how such a river network looks at this higher level. The edges do not conform to how the channels are exactly located in space, but they are representative of the general relative positions of the channels, similar to how the London Underground map contains information on the routes and intersections of all the lines, without mapping each contour & curve of the rails themselves.

Branching of channels is simple to represent in this network view. We can simply take an edge, insert two nodes in series in the middle of it, and create two distinct edges that travel between those new nodes. Each of these new edges holds half the volume of the initial edge, thus conserving volume through the network.
The image below shows the effect of many random branchings on the original network from above. We can even get nested branching within branches as seen on the far-left of the image. Branching the abstract network is simple, applying it to the river channels in space is harder to achieve realistically, as I'll get to later.
Finally merging can also be represented in this abstract representation. Merging is harder to simulate at the network level as we must handle the removal of cycles and the pruning of vestigial edges and nodes in the tree.
When two edges are merged, a new node is inserted with both the original edges as incoming nodes. I decided to only include one outgoing node from the original two on a merge, to simulate the fact that rivers eventually choose only one downstream channel which captures the entire flow at the confluence. The chosen remaining outgoing edge is the one that had the higher initial flow volume.
If, after a merger, there is a cycle in the graph, then the offending edge that joins to its own upstream channel is removed.
After these operations, it is possible for there to be edges & nodes with zero volume flowing through them because they have become detached from the sources of flow. These edges and nodes are removed until the entire graph contains non-zero flow again.
Applying random mergers to the branched graph above gives us the graph below. Note that there are no cycles and the volume is conserved at each junction but we can still get complex interactions between the different channels.
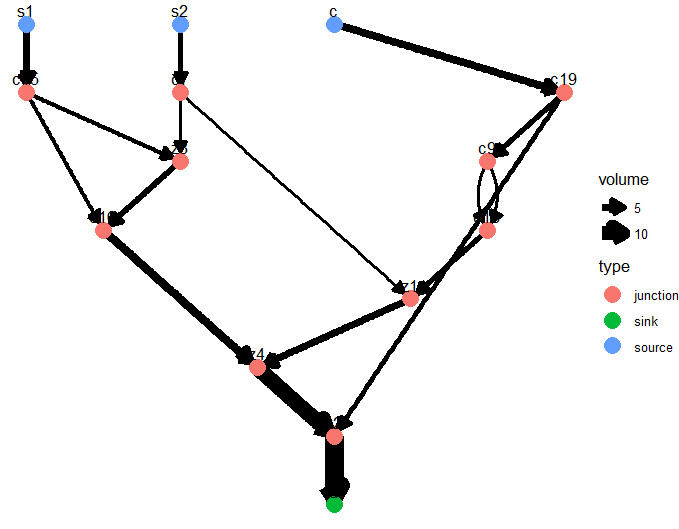
The exact shape of the channels represented by each edge are derived from relevant portions of the parent edges that produced a merger.
The characteristic length-scale of meanders should be proportional to channel width. In order to incorporate this I calculated the local curvature over a spanning window proportional to the flow volume in the chosen edge. This had the effect of making meanders larger & slower to evolve.
Combining all of this, we get the river evolution in the gif below:
Mergers between channels are easy enough to simulate in space because you can just take the incoming channel shapes and cut them at the right points to create new channels that evolve nicely with no further input needed. Unfortunately, making new branched channels was not so easy.
The problem was that branched channels would inevitably want to re-merge very quickly through a collision, at which point one channel would survive and one of the branched portions would disappear. I did not want to be giving branched channels all sorts of bespoke rules to govern their behaviour and so I gave up on implementing them in this simulation.
One separate effort that I made, was to generate branching by representing a river channel as many parallel sub-channels that repelled one another by different amounts. When the distance between two of these sub-channels was large enough then a gap would form between them which could be interpreted as a branching in the main channel.
This could produce a reasonable approximation of braided channels, but was sufficiently difficult to work into my original simulation that I left it for now. If I were to revisit this, then extending the simulation to accurately include the generation and evolution of branches in an emergent and physically motivated way would be the next step I would take.
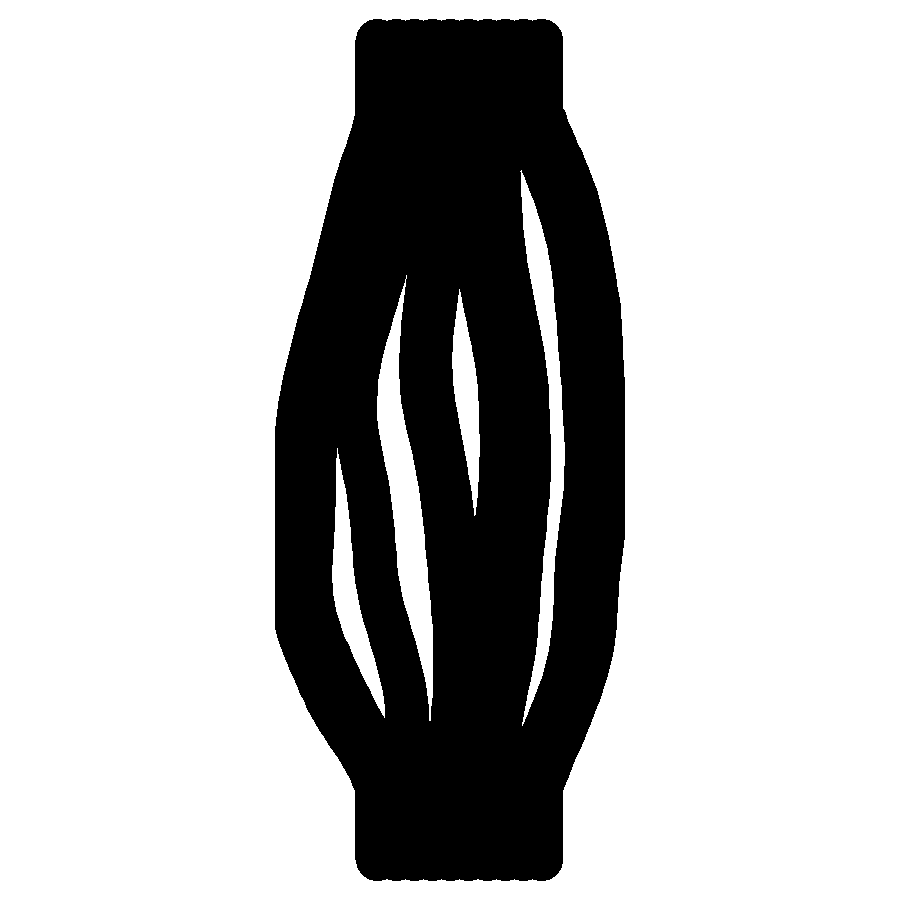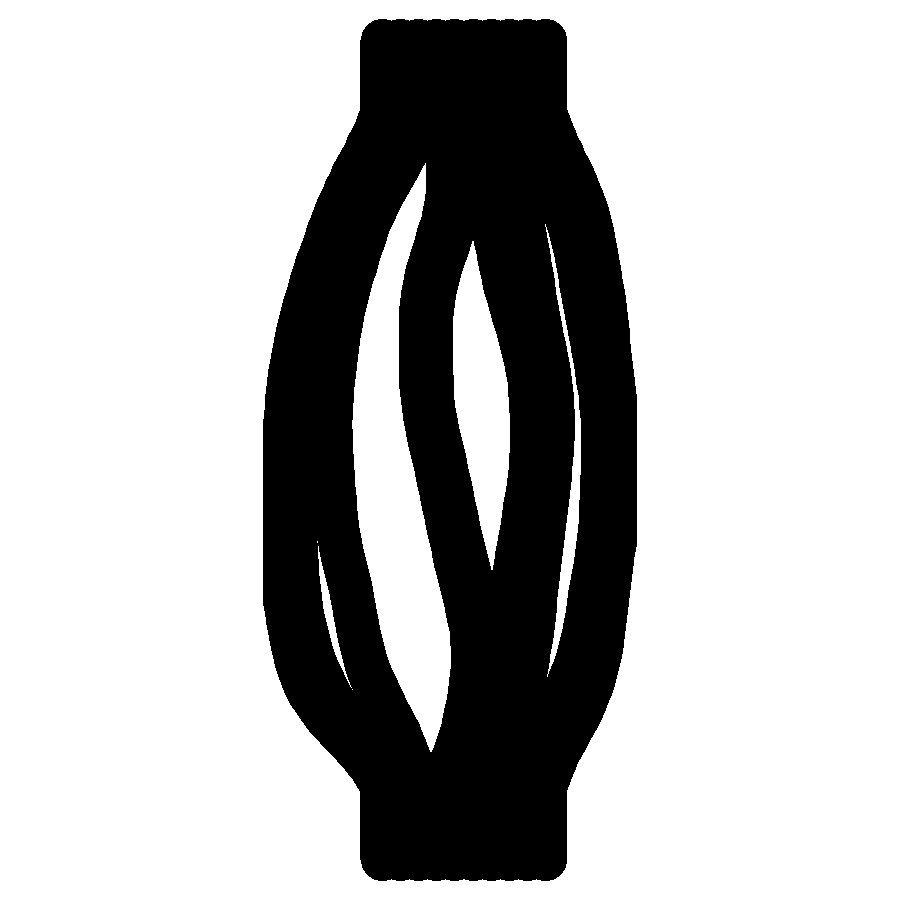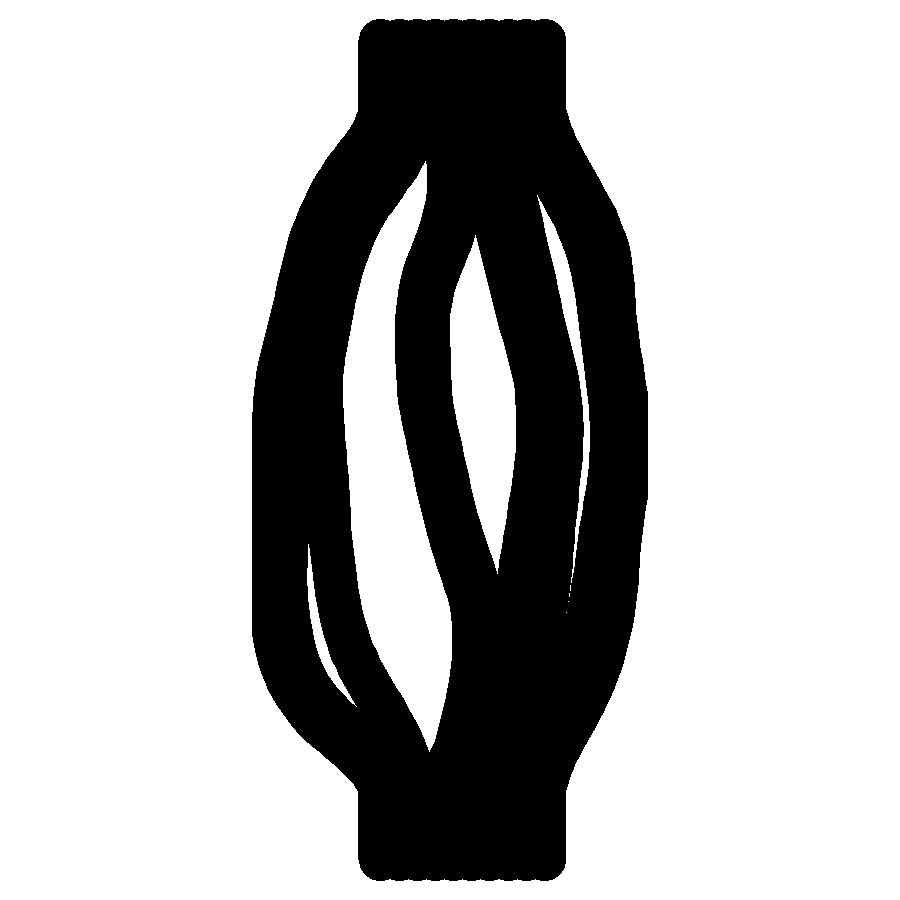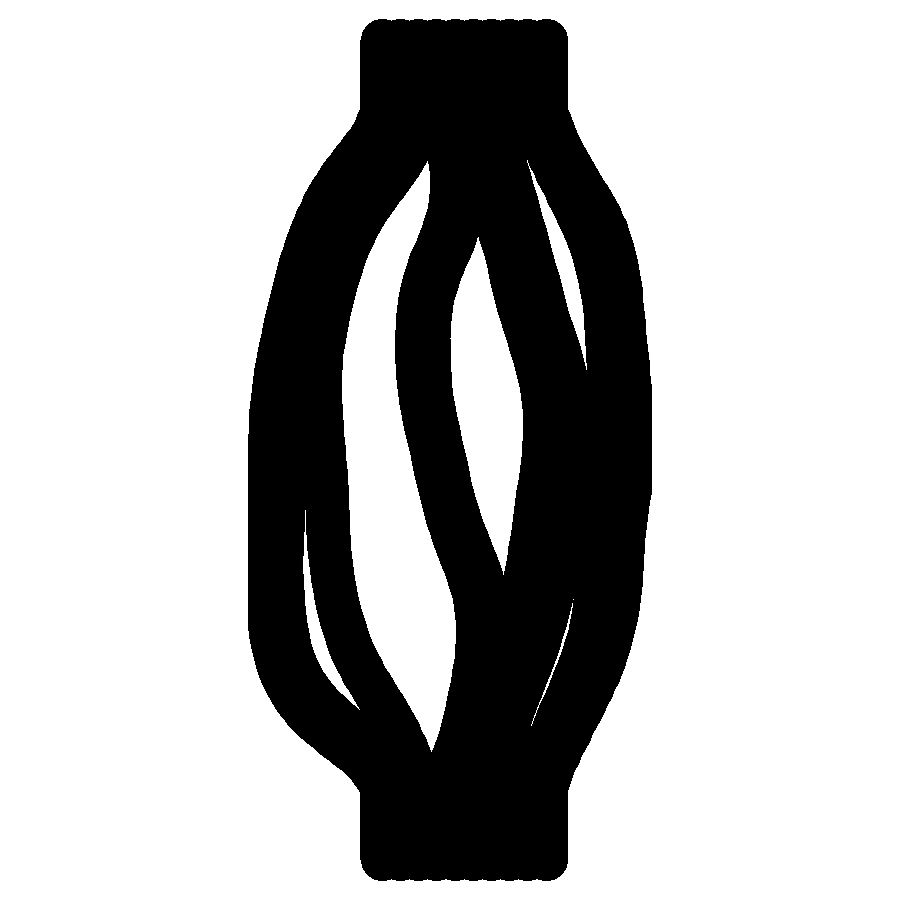
I wanted to produce a gallery of images of my simulated rivers, like Fisk's Mississippi maps. I generated a series of elevation maps that had mountains at the bottom and a flat plain at the top. Rivers were generated on the upper slopes of the mountains and left to evolve, meander, and merge following the rules that I defined above. This created a diverse set of river histories.
I then plotted these rivers in layers. The first layer of the image was the elevation map, with contours and colouring showing the mountain heights. Next the oldest river snapshot was added. Each subsequent set of river locations was plotted over the top, creating a colourful narrative of how meanders formed and were abandoned, and formed again, and how tributaries merged over time to occasionally form a vast channel which drained every source on the entire map.
A few examples are included below, but the full set can be found at the link below




This project was a little less emergent than I would normally want, I had to explicitly prescribe much of the simulation behaviour to achieve the results that I wanted. This saved lots of time and computational energy compared to a simulation of the underlying physics of rivers but allowed me to actually produce results, which is no guarantee with a tougher project. I (masochistically?) programmed this in R because it is the language that I am most familiar with and I have the most confidence in plotting. Perhaps on my next project I'll finally make the leap to C++
I hadn't previously had much experience with graph algorithms before, this was a nice sandbox to experiment with them.
I was able to both accelerate and decelerate my progress on this project by using LLMs. I found it most helpful to use them to craft short, specific functions where I would provide the input and output data formats and say exactly what I wanted it to do. It would go overboard handling numerous exceptions which would never occur in practice, but the code would work straight away a fair fraction of the time. They were least helpful for the grand-strategy of the project, leading me on wild goose chases regarding the data structures that I was to use, and when attempting to fit more than a couple of functions together, things would start to break down.
At the current moment, it seems most fruitful to keep the high-level details solely at the human level, with AI used to tinker with local parts of the code in a controlled manner.
